For comments, feedback and topic suggestions, please send a mail to chanrt.visualize@gmail.com or tweet me @_chanrt_
Filter by Subject:

Ising Model
Explore the Ising Model of Ferromagnetism. Tweak parameters like temperature and interaction strength, and see how the system evolves in real-time! Learn how the simulation works.
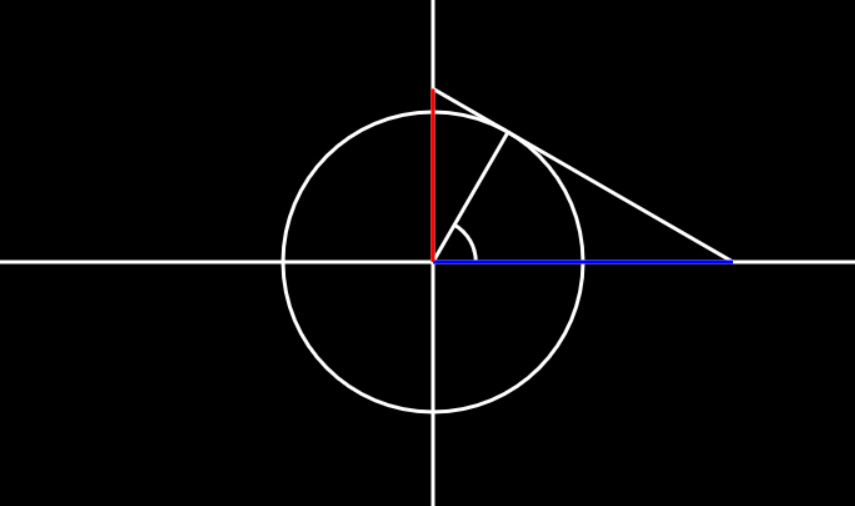
Trigonometric Functions
Does trigonometry still bring in the sweats? Or do you want to intuitively understand it? Whatever be the case, this interactive visualization provides a highly intuitive and visual understanding of all six Trigonometric functions, their properties and identities.

Ant Colony
Ant Colony Optimization (ACO) is an interesting way to obtain near-optimum solutions to the Travelling Salesman Problem (TSP). This simulation allows you to change the optimization parameters in real-time to notice their effects
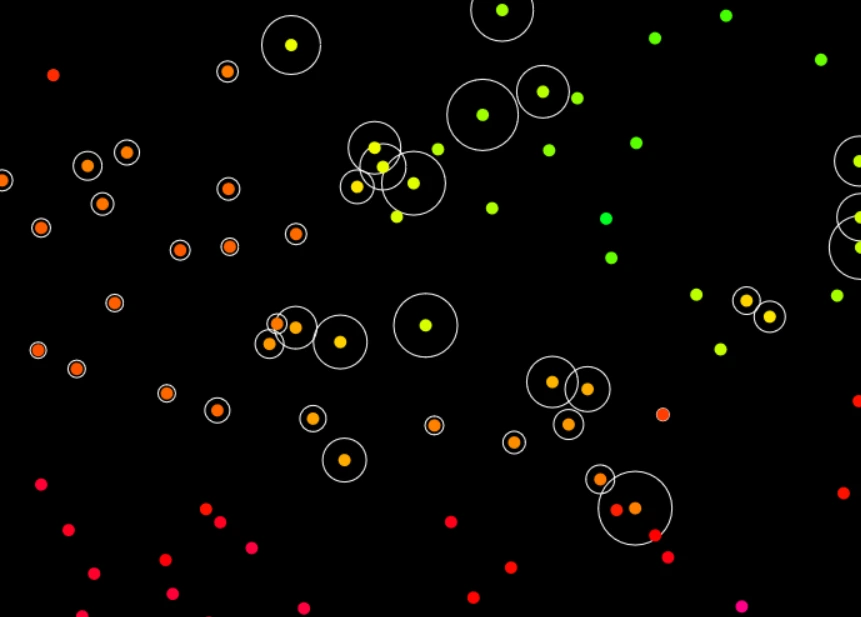
Firefly Sync
Fireflies have an internal clock on the basis of which they emit light periodically. However, they manage to sync up their cycles by observing their neighbours and nudging their phase accordingly. See this mechanism in action!
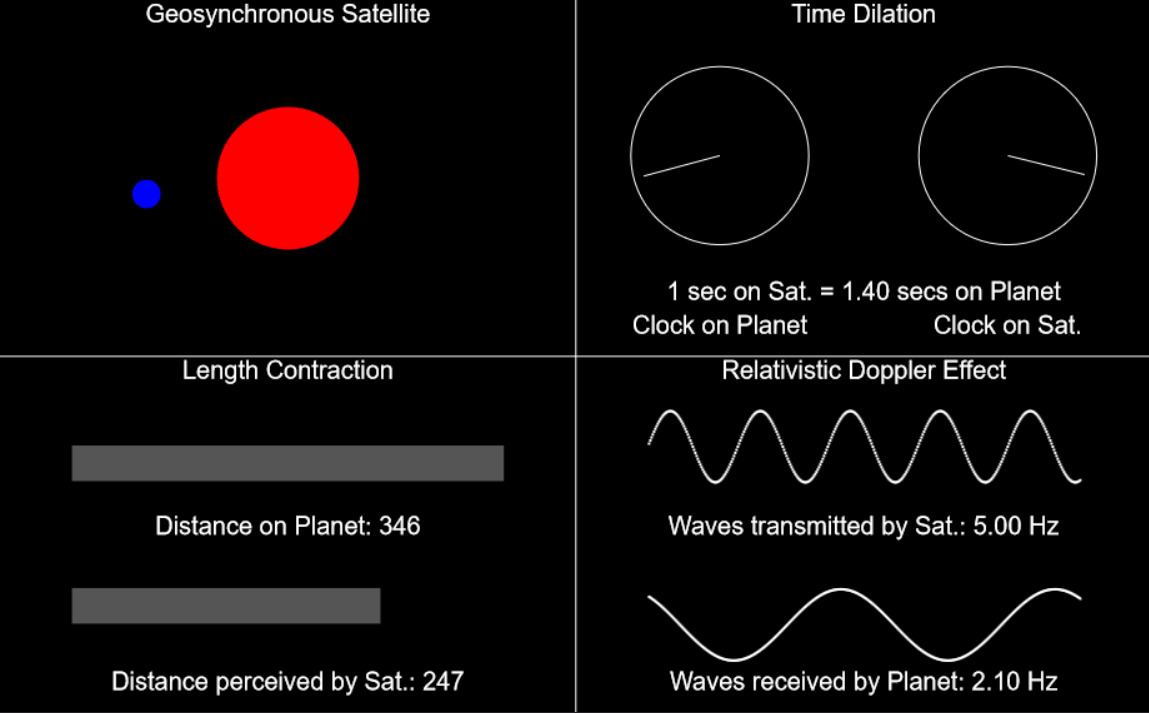
Special Relativity
Find out what Einstein's 1905 brain-child is about. Make your vehicle move as fast as you want (but within physical limits) and view Time dilation, Length contraction and Relativistic Doppler Effect in action.
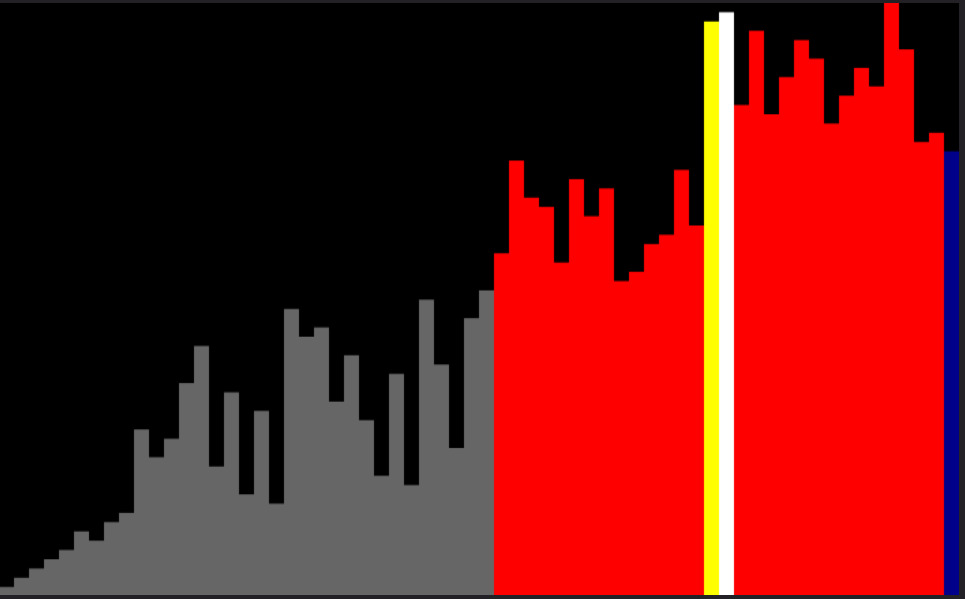
Sorting Algorithms
View the working of 7 sorting algorithms, step by step, alongside some juicy info! This simulation also shows you operational parameters like number of array accesses and comparisons.

Collective Behaviour
Simple interactions like repulsion, orientation and attraction, can operate to different extents adn give rise to a variety of collective behaviours. Learn about swarms, swirls and flocks!
Game of Life
Can a simple set of rules give rise to complex behaviour? Conway's Game of Life is also based on a simple set of rules, put forth by John Conway in 1960s. From simple patterns like Gliders, to self replicating entities and Turing complete computers have been devised in Conway's universe.

Hopfield Networks
Hopfield networks are simple constructs that are capable of learning and recalling patterns dynamically. Learn about how these processes are implemented, alongside an actual Hopfield network!
Schelling's Model
Schelling's Model is a simple agent-based model that replicates the segregation that takes place in populations with different backgrounds or opinions. This interactive simulation allows you to vary different parameters!
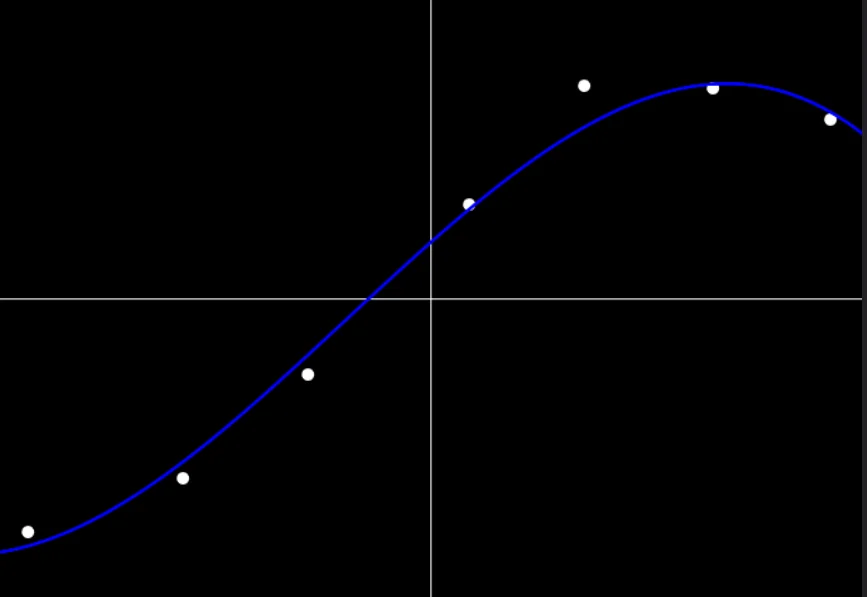
Gradient Descent
The Gradient Descent algorithm is the powerhouse of machine learning. Regression models as well as neural networks use this algorithm to optimize their working according to the training examples. Experience it first-hand!

Mandelbrot Fractal
The Mandelbrot Fractal ought to erase any doubts about the beauty of Math. It is amazing how a simple iteration (f(z) = z2 + c) can give rise to such complex, intricate, self-repeating patterns. Zoom in and explore the beautiful sights!

Lotka Volterra
The Lotka Volterra Model is a simple predator-prey model that can be used to study the interactions between two species. This simulation is a spatial version of the same model. Vary the model parameters and see how the populations of the species change over time.
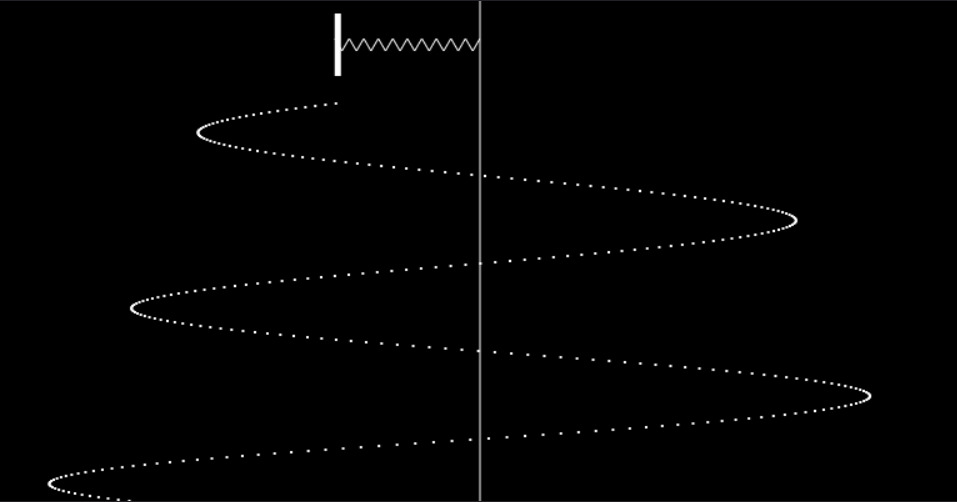
Spring Motion
Springs: the simplest non-linear physical system whose working is intuituvely obvious. Vary all parameters, from spring constant to dispersion! View damped oscillations in action!

Bernoulli Percolation
Bernoulli percolation is the simplest model that features a phase transition. This interactive simulation allows you to witness this phase transition in real time.
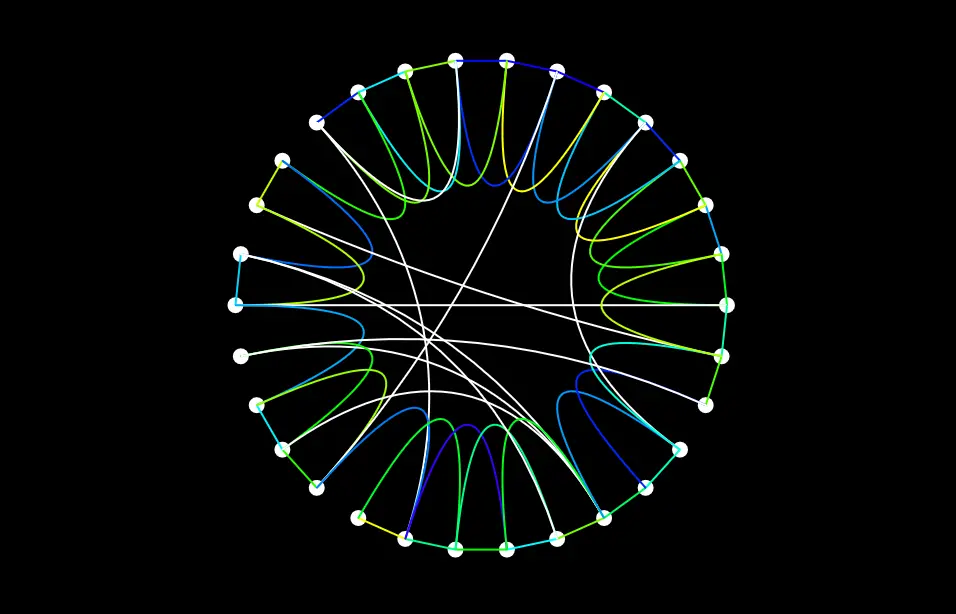
Small-World Networks
Small-world networks represent the middle-ground between regular lattices and random graphs. They have many interesting properties, and a lot of real-world interactions resemble small-world networks. Explore this topic in an interactive manner!
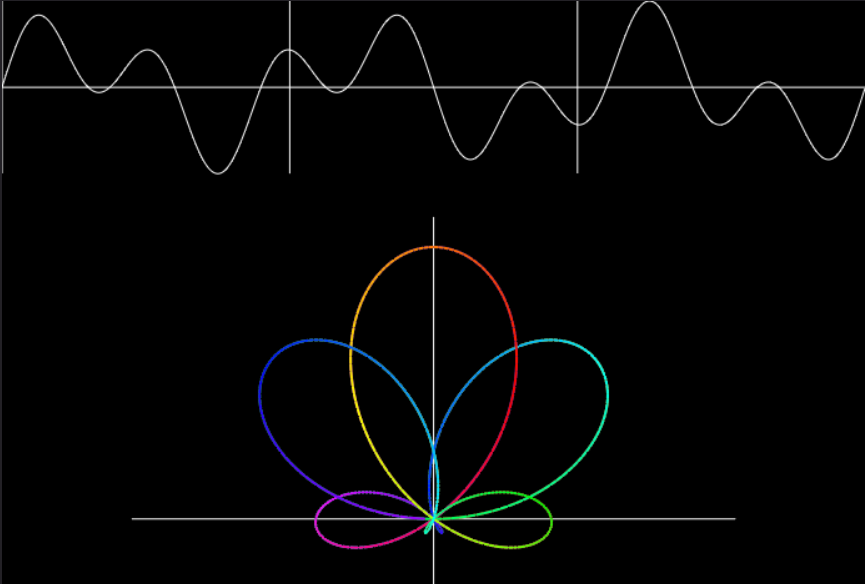
Fourier Series
The concept of Fourier Transforms and Series are pervasive in the fields of science and technology, yet its understanding is impeded due to its cryptic nature. This visualization attempts to rectify that, by providing a framework to better understand this topic.

Image Filters
Simple matrix operations on RGB values of an image can transform various aspects of the image or yield useful information. this interactive visualization allows you to apply your own kernels to a collection of images.

Lorenz System
Ever come across the term "Butterfly Effect" in the context of chaos? It is generated by the Lorenz system of equations. Vary the parameters a little and see the trajectory change a lot! Come across the set of equations that generate these patterns.
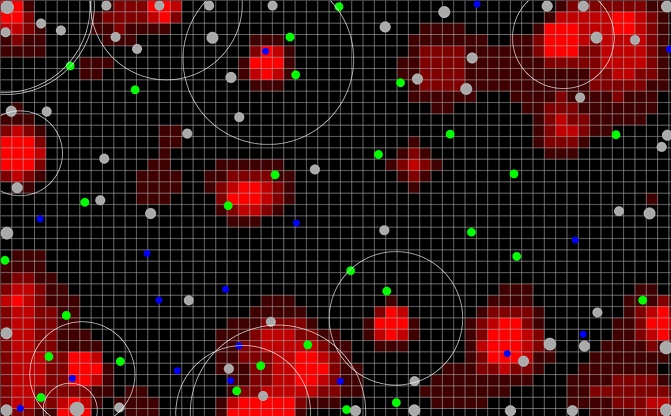
Nuclear Fusion
This simulation attempts to recreate the conditions under which Nuclear fusion takes place. Efficient and sustainable nuclear fusion will be revolutionary to our energy sector and change the future of our species!

Vicsek Model
Vicsek model is a simple agent-based model that describes the behaviour of self-propelled entities. This model is also known to show a phase transition from disordered has to ordered fluid. Fiddle around with this interactive simulation.
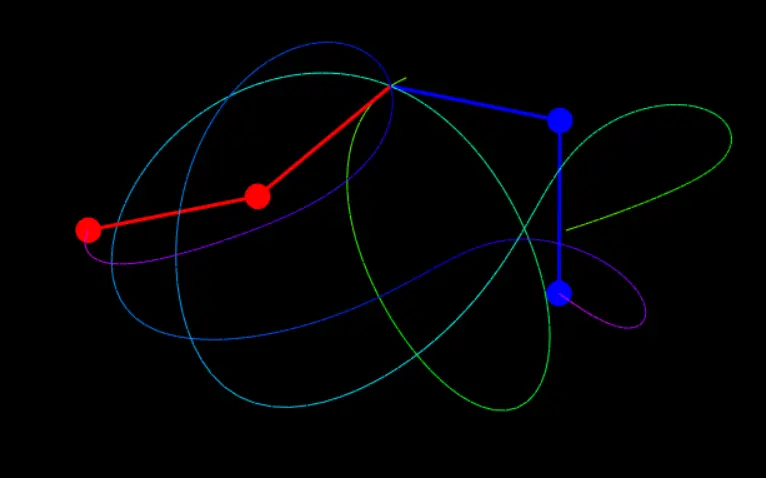
Double Pendulum
Double pendulum is a simple system that exhibits deterministic chaos. This simulation showcases why it is meaningless to predict long-term behaviour of chaotic systems.

Public Goods
A public good (eg: lighthouse) is any service that is non-excludable and non-exhaustible. Yet, one requires resources for their establishment and maintenance. This simulation explores a circumstance when public goods can be maintained even when free-riders are untraceable
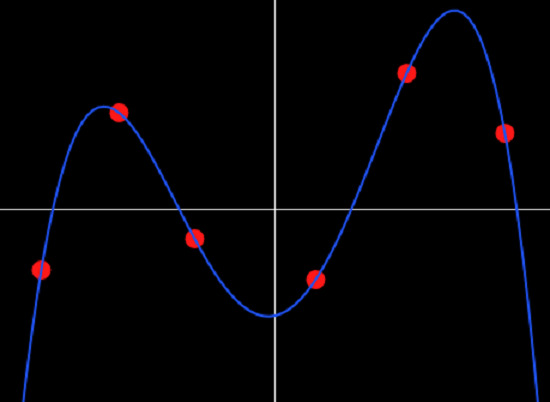
Polynomial Regression
Polynomial Regression is the process of fitting a bunch of points to a polynomial of a given order. It forms the basis for several Machine Learning algorithms. This simulation allows you to define your own points and find the best fit using the polynomial of the given degree.

Reaction Diffusion
A complex spatio-temporal model known to generate beautiful and intricate patterns! Reaction Diffusion systems have various uses in chemistry, physics, biology and ecology. This simulation allows you to draw on the canvas and watch both reaction and diffusion in action!

Hilbert Curve
Is it possible to traverse through entire space with a line that doesn't cross itself? Hilbert curve is a 2D space filling curve that does the job. Increase the order to see the curve progressively fill up the entire space.

Pedestrian Dynamics
This simulation showcases how lane formation as well as phantom traffic james happen in a crowd of pedestrians who merely want to avoid crashing into each other. Explore how bias in direction and variance in speed affects the flow of the crowd.
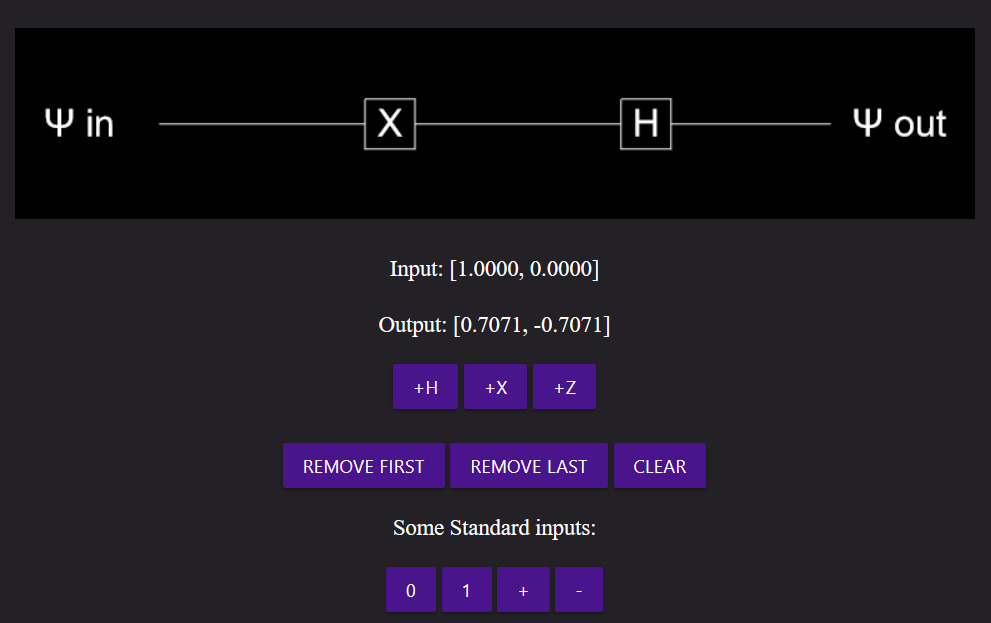
Quantum Computing
Quantum Computers are expected to beat classical computers at solving certain classes of problems. They can easily simulate quantum systems too. In this simulation, play with the building blocks of Quantum Circuits!
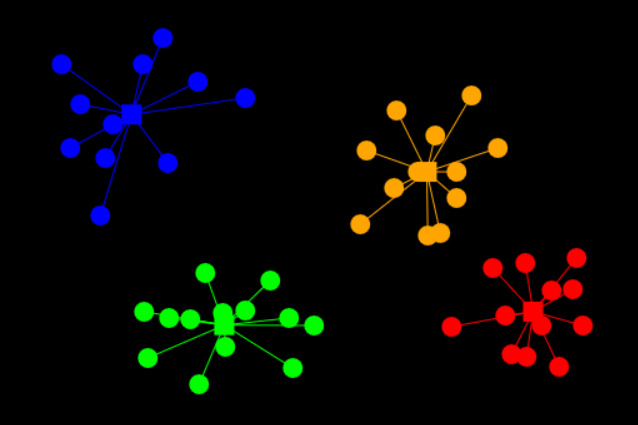
Clustering
Explore the working of k-means clustering algorithm, with a hands-on simulation. This algorithm is widely used in unsupervised machine learning.

Contact Process
A randomized cellular automaton that is widely used in percolation theory and extinction theory, to approximate mean-field models in various fields of science.
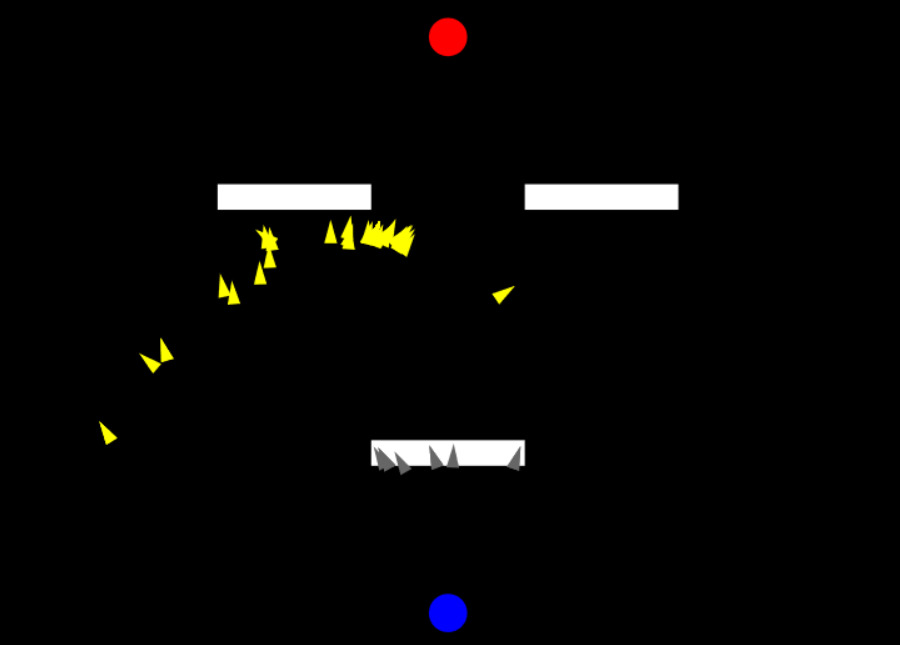
Genetic Algorithm
View the process behind the diversity of lifeforms we see today! This simulation utilizes an Evolutionary Algorithm to select the boid with the best genes. Change the positions of the source, target and the obstacles to build your own custom worlds!

Simple Fluid
This is an attempt to simulate fluids for educational and aesthetic purposes. Obtain a simplified understanding of the Navier-Stokes equation!
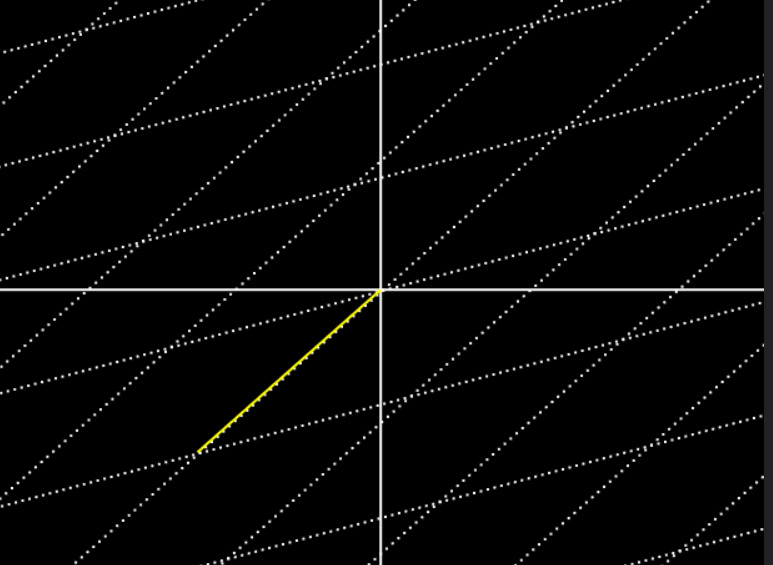
Linear Transforms
Play around with the operation that is central to linear algebra. The coordinate system is your playground. Scale, rotate and skew! Encounter rotation matrices and inverses. See what a matrix with zero determinant does to the linear space.
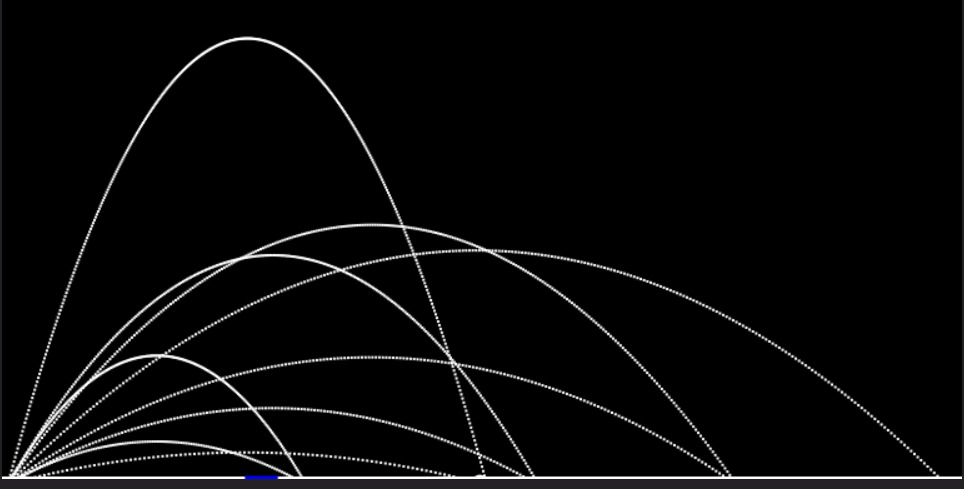
Projectile Motion
An everyday example of 2D motion. Explore projectile motion through the lens of a game. Try to hit the blue target with the correct initial velocity and angle!
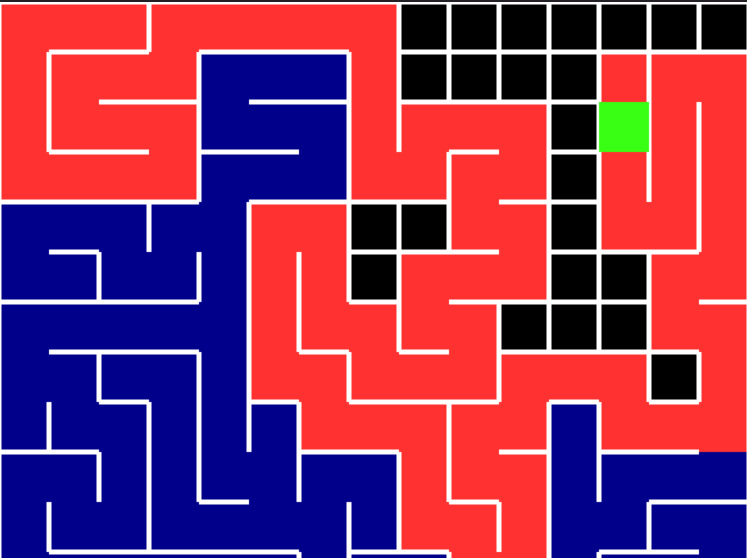
Maze Generation
Ever wondered how maze generation algorithms work? This simulation encompasses three maze generation algorithms (as of now). Also found brief description of the step-by-step working of these algorithm, along with their pros and cons.
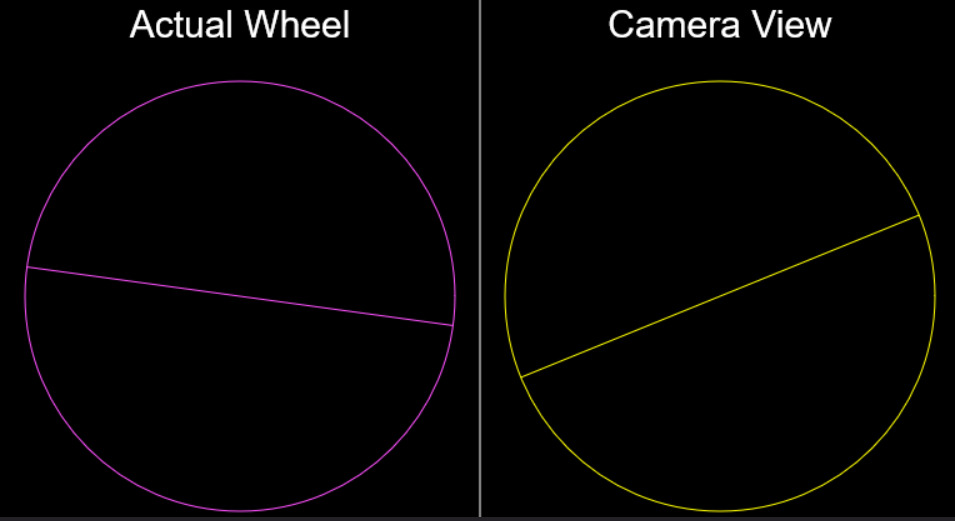
Stroboscopic Effect
Haven't you observed weird stuff happening with rotating objects? A reversal of direction? Spokes rotating slower than they ought to? Or a flying helicopter with stationary rotors? This simulation explains and showcases this illusion.

Monte Carlo
Gain the intution behind Monte Carlo simulations by using it to quickly estimate the value of pi using nothing except random numbers! Monte Carlo simulations allow us to obtain numerical results from randomness.
Linear Momentum
The conservation of linear momentum is a central topic in all avenues of Physics. Observe the computer AI crush you repeatedly at Pong by using this concept!

Porous Percolation
This simulation visualizes the percolation of fluid through a porous medium. Change the porosity of the medium, and witness a sharp transition that takes place at 0.59!
Bezier Curve
Computers use Bezier curve to render all text based elements. Further, they are widely used in designing and computer graphics. Design your own curves using this simulation! Use as many control points as you wish!
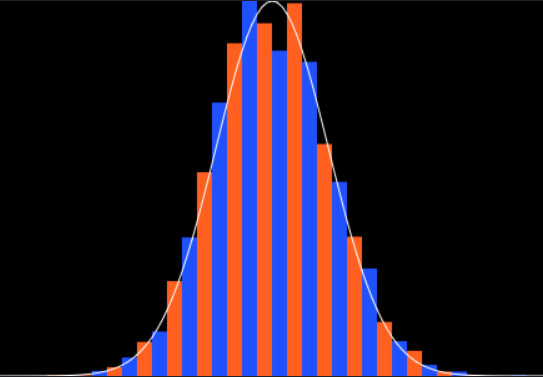
Random Walks
Explore the subtle relationship between unbiased random walks, binomial distribution, central limit theorem, Pascal's triangle and normal distribution. Simulate thousands of animals walking any distance you want and analyse their distribution!
Planetary Motion
The Law of Universal Gravitation is aptly named. Put forth by Isaac Newton in 1687, it describes the motion of every massive particle in the universe. Play around this framework with as many bodies as you like!

Directed Percolation
Tricritical Directed Percolation (TDP) is a simple probabilistic model that can be used to study vegetation dynamics. This model features continuous and abrupt transitions. Witness them in real-time.

Lexical Analysis
Lexical Analysers convert user-written programs into tokens, before being passed on to the compiler. Explore the working of a simple lexical analyser!
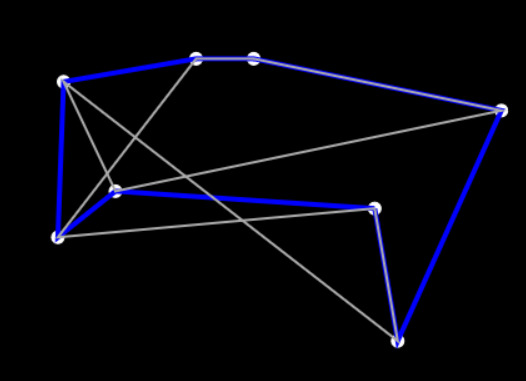
Travelling Salesman
A salesman wants to cover all places of interest through the shortest path possible and without visiting the same place twice. What path should he follow? This deceptively simple looking problem becomes extremely diffucult to solve as the number of places increases!
Developed by Chandan Relekar | Fork me at GitHub